Introducción al estudio de la estructura social a partir de R

III Jornadas de Sociología - Universidad Nacional de Mar del Plata

José Rodríguez de la Fuente

Instituto de Investigaciones Gino Germani (UBA-CONICET)

3/15/23

Programa del taller

  1. ¿Qué es la estructura social?
  2. ¿Por qué usar R?
  3. Introducción (breve) a R
  4. Trabajando con encuestas de hogares: EPH
  5. Construyendo variables: las clases sociales
  6. Explorando resultados. Tablas y gráficos
  7. Dudas y consultas

Bibliografía recomendada

1. ¿Qué es la estructura social?

¿Qué es la estructural social? (1)

  • Carácter temporal: relaciones estables de la sociedad, regularidades de sus elementos constituyentes.

  • Carácter plural: designa los rasgos de grupos y sociedades, en otras palabras, que excede a los aspectos individuales.

  • Puede abordarse desde diversas dimensiones: económica, social, política, etc.

¿Qué es la estructural social? (2)

  • La estadística es una disciplina central para el estudio de la estructura social
    • Da cuenta de la variabilidad de la vida social humana
    • Permite dar cuenta de la regularidades poblacionales (junto con la teoría)
  • Importancia en cómo los datos son recogidos y analizados

¿Estructura social o estructura de clases?

Al hablar de clases hablamos de la estructura socio-económica (aunque a veces se usen cómo sinónimos)

  • Existen distintos enfoques:
    • (neo)marxista
    • (neo)weberiano
    • Funcionalista
    • Bourdiano
    • Estadístico / pragmático

Todos deben poder ser operacionalizados
😒

2. ¿Por qué usar R?

Ventajas

  • Código abierto: amplia cantidad de paquetes
  • Es gratuito
  • Gran comunidad de usuarios (foros)
  • Uso extendido en la ciencia (sociales) y ámbito profesional
  • Trabaja con la memoria virtual
  • Capacidad de armar tableros, aplicaciones, documentos, etc.

Desventajas (1)

  • Las órdenes deben darse por sintaxis (no hay mucho point and click)
  • Hacer cosas sencillas y rápidas puede llevar más tiempo que en otros programas
  • La curva de aprendizaje es lenta

Desventajas (2)

Desventajas (3)

Comparaciones con otros programas

Software Interfaz Curva de aprendizaje Manipulación de data Análisis estadístico Gráficos Especialidades
SPSS Menus & Sintaxis Gradual Moderada Alcance moderado
Baja versatilidad		 Buenos Tablas personalizadas, ANOVA & Análisis multivariado
Stata Menus & Sintaxis Moderado Fuerte Amplio alcance
Media versatilidad		 Buenos Análisis de panel, Análisis de encuesta & Imputación múltiple
R Sintaxis Empinada Muy fuerte Muy amplio alcance
Alta versatilidad		 Excelentes Paquetes de gráficos, Web Scraping, Machine Learning & Predictive Modeling

Fuente: https://sites.google.com/a/nyu.edu/statistical-software-guide/summary

Ejemplos de usos de R en el ámbito público y académico

3. Introducción (breve) a R

Descarga e instalación

  1. Debemos instalar R desde CRAN (the comprehensive R archive network)

  2. Debemos instalar RStudio

    • Es un ambiente de desarrollo integrado (IDE) para programar en R

  3. Recomendación de actualizar ambos programas periódicamente

Partes de RStudio

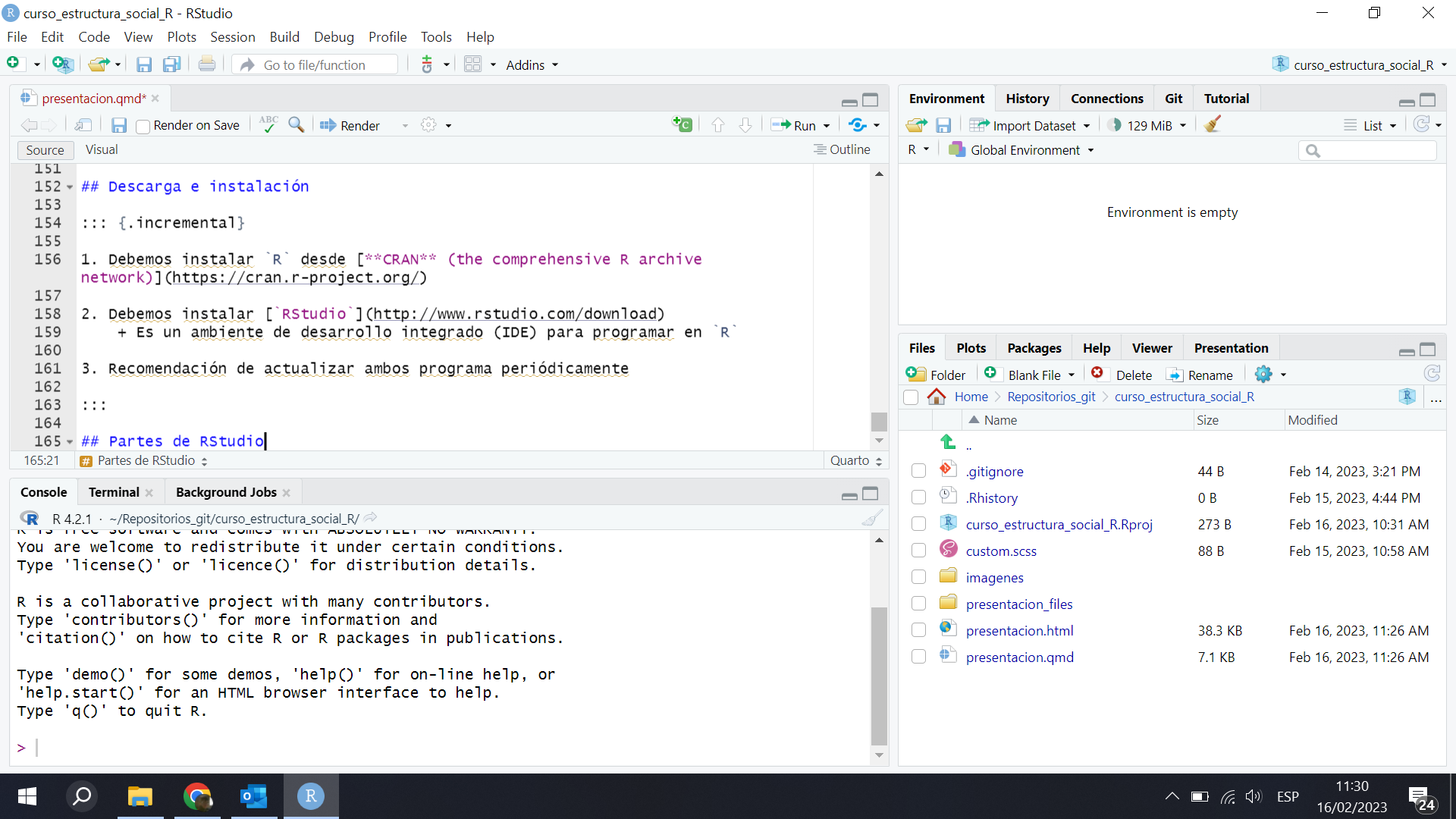
Archivos del proyecto

Ambiente de trabajo

Consola

Script o sintaxis

¿Cómo hacer funcionar R?

  • Mediante R base: comandos y funciones básicas que ya vienen incorporadas en el programa

  • Mediante paquetes:

    • Conjunto de comandos y funciones elaborados por usuarios
    • Facilitan el trabajo

¿Cómo instalar y hacer funcionar los paquetes?

  • Los paquetes se instalan via descarga de internet
  • La operación se hace directamente desde la consola o script de RStudio
install.packages("tidyverse")
  • Siempre que necesitemos usar un paquete debemos activarlo
library(tidyverse)

Flujo de trabajo: Dinámica

Fuente: Wickham and Grolemund, 2016

Fuente: https://teachdatascience.com/tidyverse/

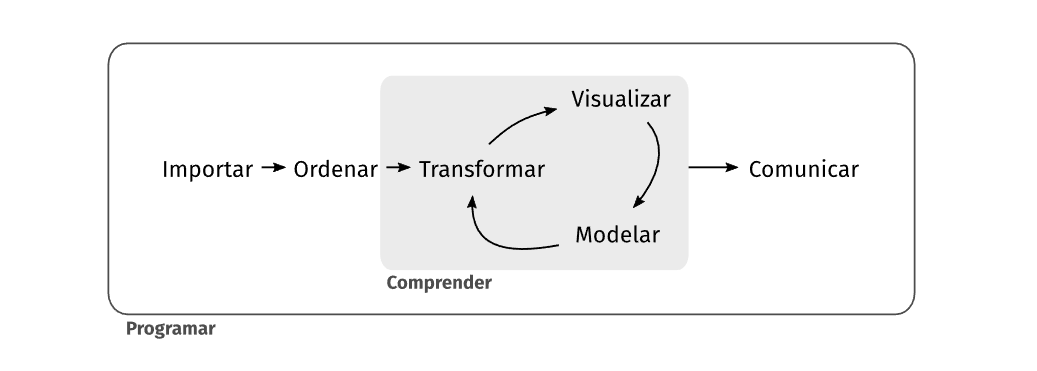
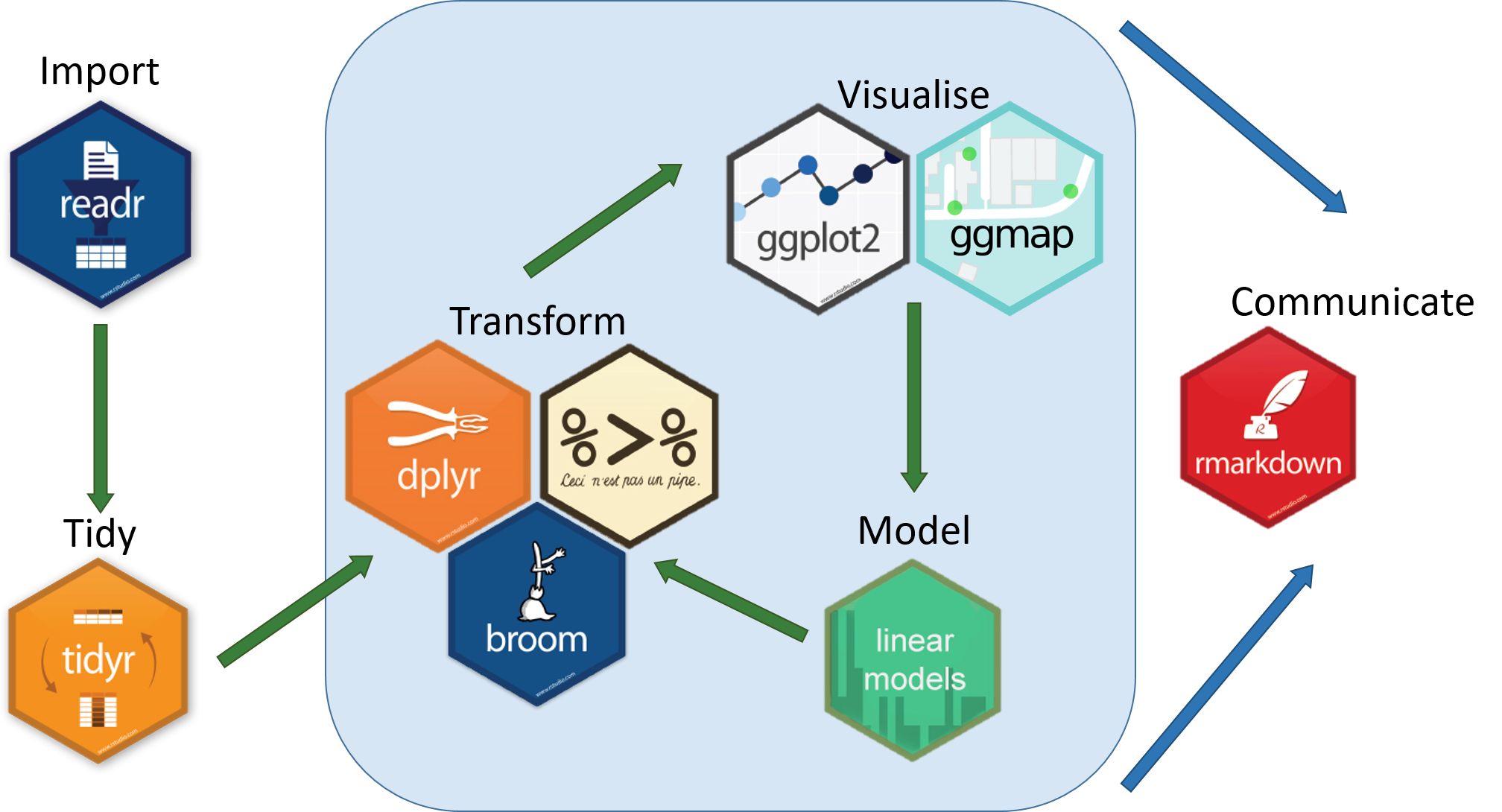
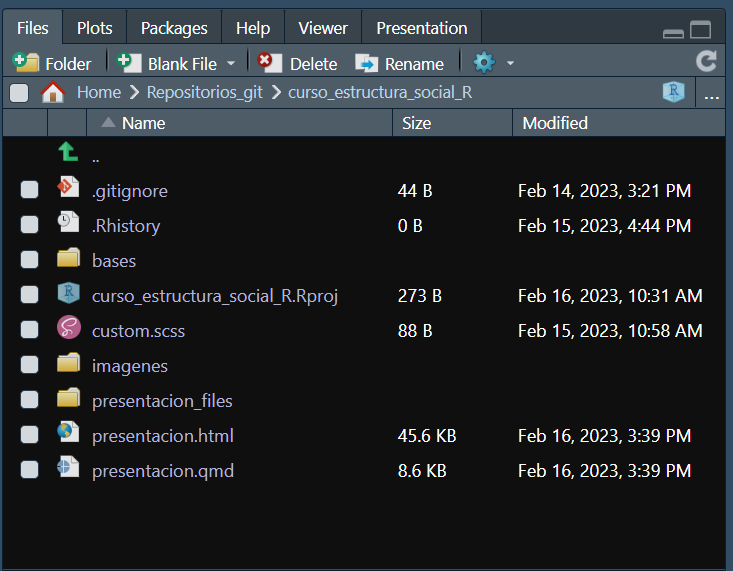
Flujo de trabajo: Proyectos

  • Siempre es recomendable trabajar dentro de un proyecto
  • Nos aseguraremos que todos los archivos y carpetas necesarios estén siempre en un lugar único
  • Trabajaremos con rutas relativas.

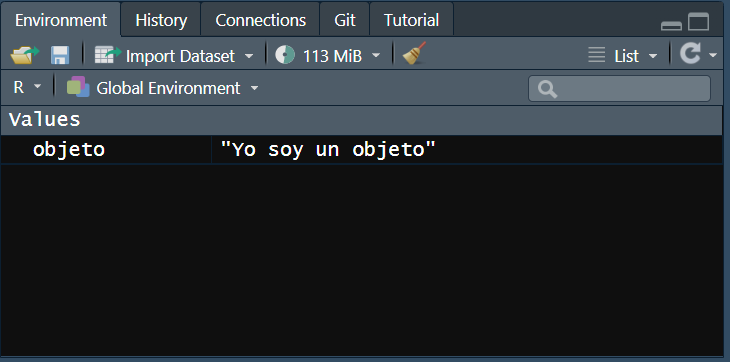
Flujo de trabajo: Objetos (1)

Todo lo que creemos en R es un objeto. Y en esto R es totalmente distinto a lo que conocíamos.


objeto <- "Yo soy un objeto"

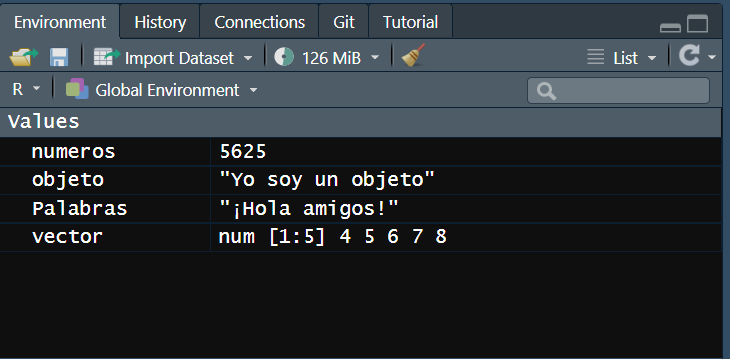
Flujo de trabajo: Objetos (2)

Podemos crear objetos a partir de:

Números

numeros <- 5625

Palabras

Palabras <- "¡Hola amigos!"

Vectores

vector <- c(4,5,6,7,8)

Listas, data frames, gráficos, funciones, mapas y muchas cosas más.

Flujo de trabajo: Elementos del script (caracteres especiales)

  • De asignación (<- o =): le asignan un valor a un objeto.
  • De anotación (#): permite escribir anotación en el script que no son leídas como código
  • Pipa (%>%): permite concatenar una secuencia de acciones sobre un objeto
    • Pertenece al paquete magrittr que está en tidyverse

Flujo de trabajo: Elementos del script (operadores)

Operadores aritméticos

  • + Suma
  • - Resta
  • * Multiplicación
  • / División

Operadores relacionales

  • > Mayor
  • >= Mayor o igual
  • < Menor
  • <= Menor o igual
  • == Igual
  • != Distinto

Operadores lógicos

  • & y
  • | ó

Flujo de trabajo: Objetos (3)

Existe una clase especial de vector denominado factor

  • Suelen ser utilizados como variables categóricas (nominales u ordinales)
  • Tienen un conjunto fijo y conocido de valores que puede asumir
  • Se suelen construir a partir de vectores de cadena


clases_sociales <- c("alta", "media", "baja", "baja", "media", "media", "baja")
clases_factor <- factor(clases_sociales, levels = c("baja", "media", "alta"))

table(clases_factor)
clases_factor
 baja media  alta 
    3     3     1

Principales funciones de dplyr

  • Filter: filtrado de filas o casos
  • Select: selección de columnas o variables
  • Arrange: ordena los casos de una variable(s)
  • Count: cuenta casos
  • Mutate: crea nuevas columnas o variables
  • Group_by / summarize: agregan casos por variable

4. Trabajando con encuestas de hogares: EPH.

La Encuesta Permanente de Hogares (I)

  • Programa nacional de producción sistemática y permanente de indicadores sociales que lleva a cabo el INDEC.
  • Comenzó a aplicarse desde 1973, bajo una modalidad (puntual) que implicaba un doble relevamiento anual (mayo y octubre).
  • Actualmente cubre a 31 aglomerados del país y se realiza bajo una modalidad continua.

La Encuesta Permanente de Hogares (II)

  • Las principales dimensiones relevadas son:
    • situación laboral 🏭
    • características demográficas básicas 🚹 🚺 🚺
    • migración 🌎
    • características habitacionales 🏡
    • educación 🎓
    • ingresos 💸 💸
  • Presenta un diseño de tipo panel (2-2-2).

¿Por qué usar la EPH para estudiar la estructura de clases?

  • Medición precisa de variables laborales
    • Ocupación, rama de actividad, sector de actividad, categoría ocupacional, tamaño del establecimiento, etc.
  • Relevamiento continuo y generalizado
    • Información desde 1974
    • Incorporación de aglomerados con el paso del tiempo
  • Relevamiento de otras dimensiones relevantes

Las bases de microdatos

Dependiendo del período que necesitemos analizar, encontraremos que las bases a descargar se encuentran en distintos formatos de archivo.

  • 1974-2002 ▶️ ▶️ .dbf ▶️ ▶️ foreign
  • 2003-2015 ▶️ ▶️ .sav .dta .xls ▶️ ▶️ haven
  • 2016-2022 ▶️ ▶️ .txt ▶️ ▶️ R base

Vamos a probar descargar e importar la base más reciente

Importando los microdatos (I)

  • Descargar desde el sitio web de INDEC la última base disponible.
  • Guardar el archivo en la carpeta bases del proyecto.
  • Importar la base con la función read.csv2
eph_03_22 <- read.csv2("bases/usu_individual_T322.txt", header = T)

¿Cuántos registros y variables tenemos?

nrow(eph_03_22)
[1] 49232
ncol(eph_03_22)
[1] 177

Importando los microdatos (II)

El paquete eph(I)

  • Creado por usuaries de la EPH: https://holatam.github.io/eph/
  • Permite:
    • descargar fácilmente las bases de datos
    • etiquetar variables y categorías
    • organizar pools de datos en panel
    • estimar tasas de pobreza

El paquete eph: funciones básicas

Vamos a activar el paquete eph y a descargar la base de individuos del 4to trimestre de 2019 utilizando la función get_microdata.

library(eph)
eph_ind_419 <- get_microdata(year = 2019, trimester = 4, type = "individual")


Podemos etiquetar las variables y categorías automáticamente con la función organize_labels.

eph_ind_419 <- organize_labels(eph_ind_419, type = 'individual')


Observamos las etiqueteas de la variable sexo

attributes(eph_ind_419$CH04)
$label
[1] "Sexo"

$class
[1] "labelled" "integer" 

$labels
Varon Mujer 
    1     2

Primeros pasos con la EPH: unión de bases (I)

  • Es frecuente que en el estudio de la estructura social debamos combinar el uso de información individual y de hogares
  • Para ello debemos unir las bases
  • Debemos identificar a las variables CODUSU y NRO_HOGAR para poder realizar la unión entre ambas bases
  • Siempre es recomendable unir únicamente las variables que necesitamos

Pero primero… debemos descargar la base de hogares del 4to trimestre de 2019:

eph_hog_419 <- get_microdata(year = 2019, trimester = 4, type = "hogar",
                             vars = c("CODUSU", "NRO_HOGAR", "II7", "II1", "IX_TOT"))

Primeros pasos con la EPH: unión de bases (II)

Ahora si estamos en condiciones de unir ambas bases

Para ello vamos a utilizar la función left_join del paquete dplyr que se encuentra en el tidyverse


library(tidyverse)

eph_419 <- eph_ind_419 %>% 
  left_join(eph_hog_419, by=c("CODUSU", "NRO_HOGAR"))

Primeros pasos con la EPH: filtrado

  • Casi siempre es necesario seleccionar una porción de nuestra muestra
  • Se aplican filtros por región, período, sexo, edad, situación laboral
  • Para ello utilizaremos la función filter del tidyverse

Seleccionaremos el aglomerado de Mar del Plata - Batán (34) y observamos la cantidad de casos con nrow

eph_419_mdp <- eph_419 %>% 
  filter(AGLOMERADO == 34)

nrow(eph_419_mdp)
[1] 1098

Ponderación de la muestra

  • Debido a que estamos trabajando con una muestra probabilística y representativa de la población es necesario ponderar los datos
  • Esto permite
    • Recalibrar la muestra salvando errores de sobre o subrepresentación
    • Expandir el número efectivo de casos al número total poblacional
  • Esto debe hacerse cada vez que realizamos un procesamiento (no es como SPSS) y dependerá de que operación debamos realizar (suma, promedio, tabulado, regresión, etc.)
  • Existencia de distintos ponderadores: PONDERA, PONDIIO, PONDII, PONDIH

Probemos calcular el total poblacional de Mar del Plata - Batán

eph_419_mdp %>% 
  tally(PONDERA)
# A tibble: 1 × 1
       n
   <int>
1 641039

5. Construyendo variables: las clases sociales

Las características socio-laborales

  • Los esquemas de clases sociales son operacionalizaciones de las teorías de clases.
  • Los elementos centrales para su contrucción son las variables
Principales variables socio-ocupacionales de la EPH
Variable Descripción Etiqueta Categorías
Condición de actividad Población activida o inactiva ESTADO Ocupado / Desocupado / Inactivo / Menor de 10 años
Categoría ocupacional Estatus jerárquico en el empleo CAT_OCUP Patrón / Cuenta propia / Empleado / Trabajador familiar
Ocupación Código de ocupación PP04D_COD (ocupación actual) / PP11D_COD (ocupación anterior) Ver Clasificador Nacional de Ocupaciones (CNO)
Rama de actividad Sector industrial de la ocupación PP04B_COD (ocupación actual) / PP11B_COD (ocupación anterior) Ver Clasificador de Actividades Económicas para Encuestas Socio-demográficas del Mercosur (CAES - MERCOSUR)
Tamaño del establecimiento Tamaño del establecimiento del trabajo PP04C / PP04c_99 Numérica
Note:
Fuente: elaboración propia

Condición de actividad

Permite distinguir entre personas económicamente activas (PEA) y no económicamente activas (PNEA)


table(eph_419$ESTADO)

    0     1     2     3     4 
   42 24441  2031 23530  8475

Ocupación (I)

  • INDEC utiliza el Clasificador Nacional de Ocupaciones
  • Este se compone de 5 dígitos

Ocupación (II)

table(eph_419$PP04D_COD)

    1  1001 10111 10112 10113 10123 10131 10132 10133 10201 10202 10203 10311 
    6     8     1    24     4     1     8    19     4    18    72    16     3 
10312 10313 10314 10321 10322 10323 10331 10332 10333 10339 11131 11201 11202 
   80   108    43     1     8     8    41   205  1680     6    99     2     7 
11311 11312 11322 11331 11332 11333 11339  2001 20111 20112 20113 20123 20131 
    2     2     1   116     8    14     1     7     2     4     7     2    59 
20132 20133 20201 20202 20203 20311 20312 20313 20323 20331 20332 20333 20339 
    8     1     8    14     1     8     1   109     1   138   164   483     1 
 3001 30111 30112 30113 30119 30122 30123 30131 30132 30133 30139 30201 30202 
  119     2    20  1028     5     4    16     6    54   208     3     1    13 
30203 30311 30312 30313 30314 30319 30322 30323 30331 30332 30333 30339 31113 
   40     3    20   239   680    14     3    14    13   106   493    10    40 
31122 31123 31131 31133 31203 31312 31313 31314 31319 31322 31323 31332 31333 
    1     5     1    13     1     3    34    21     5     1    18     1    21 
31339 32113 32121 32123 32131 32132 32201 32202 32203 32313 32314 32323 32331 
    3     5     1     3     4     4     1     2     3     6   173    33     3 
32332 32333 33114 33123 33314 34113 34123 34202 34312 34313 34314 34323 34332 
   12     5   150     2    30     1   265     3     2     3    67   729     4 
34333 35113 35123 35133 35201 35202 35203 35313 35314 35323 35332 35333 36112 
    6     1     8     1     1     2     2    12    22    33     2    61     1 
36114 36202 36203 36313 36314 36323 36324 36333  4001 40111 40112 40113 40122 
   13     7     5    32   118    52     1    41     6    64    75    11     5 
40131 40132 40201 40202 40203 40311 40312 40313 40314 40321 40322 40323 40331 
   35    10     9    16     1   185   352    36    12     3    23     3   103 
40332 40333 41111 41112 41131 41132 41201 41202 41203 41311 41312 41313 41314 
   46     9     4   109     2    16     1     3     3    33   793    77     3 
41322 41331 41332 41333 42111 42131 42202 42203 42311 42312 42313 42321 42331 
    4    83   511    24     1     1     2     1    19     3     6     1    31 
42332 42333 42339 43131 43312 43331 43332 43333 44111 44113 44132 44201 44202 
    5     6     1    20     2    29    11     6     1     2     1     2     1 
44311 44312 44313 44321 44322 44323 44331 44332 45112 45122 45131 45132 45201 
    1     8    11     1     3     3     5     6     1     1     5     4     1 
45202 45312 45322 45323 45331 45332 45333 46132 46311 46312 46313 46331 46332 
    1    13    14     2    16    56     2     2     5     2    15    37     4 
46333 47113 47123 47202 47203 47303 47312 47313 47314 47323 47324 47332 47333 
    5     8     2     1     1     1     1   215    49     6     2     2    42 
48311 48312 48313 48319 48322 48323 48331 48332 48333 48339 49311 49312 49313 
   12    47   218     2     6    15     4    28    29     1     1     2    32 
49314 49319 49322 49323 49332 49333 49339  5001  5002 50111 50112 50113 50122 
   11     3     1     2     2     9     2   139   634    14     7     6     1 
50131 50311 50312 50313 50314 50321 50322 50331 51112 51132 51312 51313 51314 
    9    22     1     2     1     1     2     1    24     1    73     1     5 
51332 52112 52123 52132 52133 52202 52203 52312 52313 52314 52323 52333 53112 
    1     4     4     1     4     2     4    12    11     1     3     2     2 
53113 53123 53133 53202 53203 53312 53313 53314 53332 53333 54112 54113 54133 
  185     2     5     6    13    11   257   353     2     3     1     1     1 
54202 54312 54313 54322 54331 54332 54333 55313 55314 56113 56114 56123 56202 
    1     5     3     1     1     1    24     8  1404     5    31    11     2 
56203 56313 56314 56323 56324 56333 57112 57113 57122 57123 57132 57133 57312 
    8   116   875    30     3     1    21   283     5     1     1     2     7 
57313 57314 57323 57332 57333 58112 58113 58122 58123 58132 58133 58203 58312 
   51   458     2     2     1    12   209     1     3    18     3     1     1 
58313 58314 58322 58323 58332 58333  6001 60111 60113 60114 60123 60201 60202 
   62    53     2    16     2     4   263     1    10     1     8     1     1 
60311 60312 60313 60314 60323 60331 61111 61113 61311 61313 61314 62313 62314 
    2     1    22    90    12     1     1    26     1    16     3    30     1 
62323 63113 63203 63313 63314 64202 64313  7001 70113 70202 70203 70311 70312 
    3     4     1     1     4     1     5    92     1     7     6     2     2 
70313 70314 70322 70323 70331 70332 70333 71202 71203 71311 71312 71313 71314 
   20     5     1    15    13     3     5     1     1     2     1     6     1 
71331 71332 71333 72111 72112 72113 72114 72123 72131 72132 72133 72201 72202 
    3     3     1     2    45   785    16     8    44    13     1    12    15 
72203 72209 72311 72312 72313 72314 72321 72322 72323 72331 72332 72333 80112 
   27     1     5    49   806   498     1     6    68    49    24     7     4 
80113 80122 80123 80131 80132 80133 80201 80202 80203 80311 80312 80313 80314 
  282     6   177     1    34    13     8    18    19     3    10   495    98 
80319 80321 80322 80323 80324 80331 80332 80333 81131 81132 81201 81202 81331 
    2     1     5   430     3     6    54    39     3    25     6     1    48 
81332 82112 82113 82122 82123 82132 82202 82203 82312 82313 82314 82323 82324 
   43    44   256     1    85    11     2     2     8   185    47     9     1 
82332 82333 90112 90113 90201 90202 90203 90311 90312 90313 90314 90319 90322 
    5     4     6     5     1     3     1     1    22    66     5     1     1 
90323 90332 90333 91311 91331 91332 91339 92112 92131 92132 92201 92202 92203 
   12     4     6     1     2     1     1     3     1    26     1     5     2 
92312 92313 92323 92331 92332 92333 92339 99202 99203 99992 99993 99994 99997 
   16    58     4    16    56    18     1     2     2    18    10     1   129 
99998 99999 
    4    15

Categoría ocupacional

Permite discriminar a la población en función de su posicionamiento en las relaciones de producción y a partir del origen de sus ingresos


table(eph_419$CAT_OCUP)

    0     1     2     3     4     9 
32503  1012  5714 19127   162     1

De las clases en el papel a las clases en la computadora

  • La operacionalización implica el pasaje de conceptos teórico-abstractos a indicadores empíricos.

  • Estas clases-constructos no son clases equiparables a las que podemos percibir y comprender como existentes en la realidad social, aunque presenten probabilidades de serlo.

  • El proceso de operacionalización implica una abstracción y un recorte realizado sobre la realidad.

  • Confusión de la noción de clase con otros conceptos: estratos, grupos, sectores, fracciones.

  • Hay varias propuestas teóricas de la estratificación que fueron operacionalizadas: EGP, Wright, SIOPS, SEI, ISEI, Germani, Torrado, Portes, etc.

El esquema de clases de Torrado

Clase social

Estratos sociales

Estratos sociales

Clase alta

-

Directores de empresa

Clase media

Autónomos

Profesionales en función específica

Propietarios de pequeñas empresas

Pequeños productores autónomos

Asalariados

Profesionales en función específica

Cuadros técnicos y asimilados

Empleados administrativos y vendedores

Clase obrera

Autónomos

Trabajadores especializados autónomos

Asalariados

Obreros calificados

Obreros no calificados

Marginales

Peones autónomos

Empleados domésticos

Fuente: elaboración propia en base a Torrado (1998)

Sistema clasificatorio de la clase social

Paso 1: Punto de partida

Grupo de ocupación

Empleadores

Asalariados

Servicio doméstico

Cuenta propia y familiar sin remuneración

Sector privado

Sector privado

Sector privado

Sector privado

Sector público

Más de 5 ocupados

Hasta 5 ocupados

Más de 5 ocupados

Hasta 5 ocupados

1. Empresarios, directores de empresas y funcionarios públicos superiores

1.1

5.1

1.2

4.1.2

1.1*

11

5.2

2. Propietarios de establecimientos

3

4.1.1

4.2

3. Profesionales en función específica

2.1.1

2.1.2

2.3.1

2.3.2

2.4

2.2

4. Técnicos, docentes y supervisores

3

5.1

4.1.1

4.1.2

4.2

5.2

5. Empleados y vendedores

6.1.1

6.1.2

6.2

6. Trabajadores especializados

8.1.1

8.1.2

8.2

7

7. Trabajadores no especializados

10

10

9.1.1

9.1.2

9.2

10

8. Empleados domésticos

11

11

11

11

11

11

9. Sin especificar

12

12

12

12

12

12

12

* Modificación respecto a la propuesta de Torrado. Fuente: elaboración propia en base a Torrado (1998)

Clasificador de la Condición Socio-ocupacional (CSO)

1. Ocupación

2. Categoría de ocupación

3. Sector de actividad

4. Tamaño del establecimiento

Paso 2: Ocupación (I)

  • Debemos preparar las variables para poder trabajarlas en la operacionalización.

  • En primer lugar empezaremos por agregar ceros a los registros que tienen menos de 5 dígitos, utilizando la función str_pad del tidyverse.

  • Luego vamos a separar los 5 dígitos del CNO. Para ello utilizaremos la función str_sub del tidyverse.

  • Luego convertiremos esas variables en formato numérico.

eph_419$cno <- str_pad(eph_419$PP04D_COD, 5, pad = "0")

eph_419$cno12 <- str_sub(eph_419$cno, 1, 2) #señala que parta de la posición 1 hasta 2 del código
eph_419$cno3 <- str_sub(eph_419$cno, 3, 3) #señala que parta de la posición 3 a la 3 del código
eph_419$cno4 <- str_sub(eph_419$cno, 4, 4)
eph_419$cno5 <- str_sub(eph_419$cno, 5, 5)

eph_419$cno12 <- as.numeric(eph_419$cno12)
eph_419$cno3 <- as.numeric(eph_419$cno3)
eph_419$cno4 <- as.numeric(eph_419$cno4)
eph_419$cno5 <- as.numeric(eph_419$cno5)

Paso 2: Ocupación (II)

  • Crearemos una variable que permita agrupar a las ocupaciones del mismo modo que lo hizo Torrado.

  • Para esto generaremos la variable grupo de ocupación (GO), utilizando los dos primeros dígitos del CNO.

  • A través de la función case_when del tidyverse podremos asignarle un valor a la variable en la medida que se cumplan determinadas condiciones

eph_419 <- eph_419 %>%  
  mutate(go = case_when((cno12 >= 0 & cno12 <=4) | (cno12 == 7) ~ 1,
                        
                        (cno12 >= 5 & cno12 <=6) ~ 2,
                        
                        (cno5 == 1) & ((cno12 >= 10 & cno12 <= 20) | 
                        (cno12 == 32) | (cno12 >= 34 & cno12 <= 40) |
                        (cno12 >= 42 & cno12 <= 47) | (cno12 >= 49 & cno12 <= 54) | 
                        (cno12 >= 60 & cno12 <= 64) | (cno12 >= 70 & cno12 <= 92)) ~ 3,
                        
                        (cno5 > 4) & (cno12 == 11 | cno12 == 42 | cno12 == 43 | 
                        cno12 == 50 | cno12 == 70 | cno12 == 81 | cno12 == 91) ~ 3,
                        
                        (cno5 == 2) & ((cno12 >= 10 & cno12 <= 32) | (cno12 >= 34 & cno12 <= 54) | 
                        (cno12 >= 56 & cno12 <= 92)) ~ 4,
                        
                        (cno5 == 1) & ((cno12 == 30 | cno12 == 31 | cno12 == 41 | cno12 == 48) | 
                        (cno12 >= 56 & cno12 <= 58) | (cno12 == 65)) ~ 4,
                        
                        (cno5 == 3) & (cno12 == 40 | cno12 == 42 | cno12 == 43 | cno12 == 45 | 
                        cno12 == 91) ~ 4,
                        
                        (cno5 == 4) & (cno12 == 42 | cno12 == 43 | cno12 == 45) ~ 4,
                        
                        (cno5 > 4) & (cno12 == 40 | cno12 == 41 | cno12 == 44 | cno12 == 45 | 
                        cno12 == 46 | cno12 == 51 | cno12 == 92) ~ 4,
                        
                        (cno5 == 3) & ((cno12 >= 10 & cno12 <= 32) | (cno12 == 35) | (cno12 == 41) | 
                        (cno12 == 54) | (cno12 == 81)) ~ 5,
                        
                        (cno5 == 4) & ((cno12 >= 10 & cno12 <= 11) | (cno12 >= 30 & cno12 <= 32) | 
                        (cno12 == 35)) ~ 5,
                        
                        (cno5 > 4) & ((cno12 == 10) | (cno12 >= 20 & cno12 <= 32) | (cno12 == 35)) ~ 5,
                        
                        (cno5 == 1 | cno5 == 2) & (cno12 == 55) ~ 6,
                        
                        (cno5 == 3) & ((cno12 == 34) | (cno12 == 36) | (cno12 == 44) | 
                        (cno12 >= 46 & cno12 <= 53) | (cno12 >= 55 & cno12 <= 80) | 
                        (cno12 == 82) | (cno12 == 90) | (cno12 == 92)) ~ 6,
                        
                        (cno5 == 4) & ((cno12 == 44) | (cno12 == 49) | (cno12 == 53) | (cno12 == 57)) ~ 6,
                        
                        (cno5 > 4) & ((cno12 == 34) | (cno12 >= 47 & cno12 <= 49) | (cno12 >= 52 & cno12 <= 54) | (cno12 >= 57 & cno12 <= 65) | (cno12 >= 71 & cno12 <= 80) | (cno12 >= 82 & cno12 <= 90)) ~ 6,
                        
                        (cno12 == 33)   ~ 7,
                        
                        (cno5 == 4 | cno5 == 9) & ((cno12 == 20) | (cno12 == 34) | 
                        (cno12 >= 36 & cno12 <= 41) | (cno12 >= 46 & cno12 <= 48) |
                        (cno12 >= 50 & cno12 <= 52) | (cno12 == 54) | (cno12 == 56) | 
                        (cno12 >= 58 & cno12 <= 92)) ~ 7,
                        
                        (cno5 >= 4) & (cno12 == 55) ~ 8
                        
                        ,(cno12 == 99) | (is.na(cno12)) ~ 9))

Paso 3: Sector de actividad y tamaño del establecimiento

  • Vamos a recodificar dichas variables utilizando la función recode del paquete car.

  • El sector de actividad (pp04a) quedará recodificado en 1) sector privado y 2) sector público.

  • El tamaño del establecimiento (pp04c y pp04c99) quedará recodificado en 1) 5 o menos ocupados y 2) Más de 5 ocupados.

eph_419 <- eph_419 %>% 
    mutate(sector_act = car::recode(PP04A, "1=2; 2:3=1")) 

eph_419 <- eph_419 %>% 
  mutate(tamano = case_when((PP04C > 0 & PP04C <= 5) | (PP04C == 99 & PP04C99 == 1) ~ 1,
                            (PP04C > 5 & PP04C < 99) | (PP04C == 99 & PP04C99 >= 2) ~ 2,
                            PP04C == 0 | PP04C99 == 0 ~ NA_real_
                            ))

Paso 4: Creación del CSO desagregado (I)

Con las variables necesarias ya creadas y/o recodificadas, podemos empezar a llenar los casilleros del cuadro anteriormente presentado.

Asignación de códigos al CSO desagregado
Nº sintaxis Nº real CSO desagregado CSO agregado
1 1.1 DIREC (ER - SPR. TE>5) 1
2 1.2 DIREC (AS - SPR. TE>5)
3 2.1.1 PROF (ER- SPR. >5) 2
4 2.1.2 PROF (ER- SPR. <=5)
5 2.2 PROF (CP)
6 2.3.1 PROF (AS- SPR. >5)
7 2.3.2 PROF (AS- SPR. <=5)
8 2.4 PROF (AS- SPU)
9 3 PPE 3
10 4.1.1 TECN (AS -SPR. TE>5) 4
11 4.1.2 TECN (AS -SPR. TE<=5)
12 4.2 TECN (AS -SPU)
13 5.1 PPA (ER - SPR. TE <=5) 5
14 5.2 PPA (CP)
15 6.1.1 EAV (AS - SPR. TE>5) 6
16 6.1.2 EAV (AS - SPR. TE<=5)
17 6.2 EAV (AS - SPU)
18 7 TEA 7
19 8.1.1 OCAL (AS - SPR. TE>5) 8
20 8.1.2 OCAL (AS - SPR. TE<=5)
21 8.2 OCAL (AS - SPU)
22 9.1.1 ONCAL (AS - SPR. TE>5) 9
23 9.1.2 ONCAL (AS - SPR. TE<=5)
24 9.2 ONCAL (AS - SPU)
25 10 TMARG 10
26 11 EDOM 11
27 12 Sin especificar CSO 12
Note:
Fuente: elaboración propia en base a Torrado (1998)

Paso 4: Creación del CSO desagregado (II)

Crearemos una variable que se llame cso_desag

eph_419 <- eph_419 %>% 
  mutate(cso_desag = case_when(go==1 & CAT_OCUP==1 & tamano==2 ~ 1, 
                               go==1 & CAT_OCUP==1 & tamano==1 ~ 13, 
                               go==1 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 2, 
                               go==1 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 2, 
                               go==1 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 11, 
                               go==1 & CAT_OCUP==3 & sector_act==2 ~ 1,
                               go==1 & CAT_OCUP==2 ~ 14,
                               go==1 & CAT_OCUP==4 ~ 14,
                               go==1 & CAT_OCUP==NA ~ 14,
                               
                               go==2 & CAT_OCUP==1 & tamano==2 ~ 9,
                               go==2 & CAT_OCUP==1 & tamano==1  ~ 13,
                               go==2 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 10,
                               go==2 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 10,
                               go==2 & CAT_OCUP==3 & sector_act==1 & tamano==1  ~ 11,
                               go==2 & CAT_OCUP==3 & sector_act==2  ~ 12,
                               go==2 & CAT_OCUP==2  ~ 14,
                               go==2 & CAT_OCUP==4  ~ 14,
                               go==2 & CAT_OCUP==NA     ~ 14,
         
                               go==3 & CAT_OCUP==1 & tamano==2 ~ 3,
                               go==3 & CAT_OCUP==1 & tamano==1 ~ 4,
                               go==3 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 6,
                               go==3 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 6,
                               go==3 & CAT_OCUP==3 & sector_act==1 & tamano==1  ~ 7,
                               go==3 & CAT_OCUP==3 & sector_act==2 ~ 8,
                               go==3 & CAT_OCUP==2 ~ 5,
                               go==3 & CAT_OCUP==4 ~ 5,
                               go==3 & CAT_OCUP==NA ~ 5,
         
                               go==4 & CAT_OCUP==1 & tamano==2  ~ 9,    
                               go==4 & CAT_OCUP==1 & tamano==1  ~ 13,   
                               go==4 & CAT_OCUP==3 & sector_act==1 & tamano==2  ~ 10,   
                               go==4 & CAT_OCUP==3 & sector_act==1 & is.na(tamano)  ~ 10,   
                               go==4 & CAT_OCUP==3 & sector_act==1 & tamano==1  ~ 11,   
                               go==4 & CAT_OCUP==3 & sector_act==2 ~ 12,
                               go==4 & CAT_OCUP==2  ~ 14,   
                               go==4 & CAT_OCUP==4  ~ 14,   
                               go==4 & CAT_OCUP== NA ~ 14,
         
                               go==5 & CAT_OCUP==1 & tamano==2 ~ 9,
                               go==5 & CAT_OCUP==1 & tamano==1 ~ 13,
                               go==5 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 15,
                               go==5 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 15,
                               go==5 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 16,
                               go==5 & CAT_OCUP==3 & sector_act==2  ~ 17,
                               go==5 & CAT_OCUP==2  ~ 14,
                               go==5 & CAT_OCUP==4 ~ 14,
                               go==5 & CAT_OCUP== NA ~ 14,
         
                               go==6 & CAT_OCUP==1 & tamano==2  ~ 9,
                               go==6 & CAT_OCUP==1 & tamano==1  ~ 13,
                               go==6 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 19,
                               go==6 & CAT_OCUP==3 & sector_act==1 & is.na(tamano)  ~ 19,
                               go==6 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 20,
                               go==6 & CAT_OCUP==3 & sector_act==2 ~ 21,
                               go==6 & CAT_OCUP==2  ~ 18,
                               go==6 & CAT_OCUP==4  ~ 18,
                               go==6 & CAT_OCUP== NA    ~ 18,
         
                               go==7 & CAT_OCUP==1 & tamano==2  ~ 25,
                               go==7 & CAT_OCUP==1 & tamano==1  ~ 25,
                               go==7 & CAT_OCUP==3 & sector_act==1 & tamano==2  ~ 22,
                               go==7 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 22,
                               go==7 & CAT_OCUP==3 & sector_act==1 & tamano==1  ~ 23,
                               go==7 & CAT_OCUP==3 & sector_act==2  ~ 24,
                               go==7 & CAT_OCUP==4  ~ 25,
                               go==7 & CAT_OCUP==2  ~ 25,
                               go==7 & CAT_OCUP== NA    ~ 25,
                              
                            go==8 ~ 26,
                            go==9   ~ 27))

Paso 5: Creación del CSO agregado

Crearemos una variable que se llame cso_agg

eph_419 <- eph_419 %>% 
  mutate(cso_agg = case_when(cso_desag <=2 ~ 1,
                             cso_desag >=3 & cso_desag <=8 ~ 2,
                             cso_desag ==9 ~ 3,
                             cso_desag >=10 & cso_desag <=12 ~ 4,
                             cso_desag >=13 & cso_desag <=14 ~ 5,
                             cso_desag >=15 & cso_desag <=17 ~ 6,
                             cso_desag ==18 ~ 7,
                             cso_desag >=19 & cso_desag <=21 ~ 8,
                             cso_desag >=22 & cso_desag <=24 ~ 9,
                             cso_desag ==25 ~ 10,
                             cso_desag ==26 ~ 11,
                             cso_desag ==27 | is.na(cso_desag) ~ NA_real_))

Paso 6: El esquema final (I)

¡Ya estamos en condiciones de elaborar el sistema de clases que la autora propone!

Con la función factor crearemos una variable factor etiquetando el esquema de clases.

eph_419 <- eph_419 %>% 
  mutate(clase6 = case_when(cso_agg == 1 ~ 1,
                                                    (cso_agg == 2 & CAT_OCUP == 2) | cso_agg == 3 | cso_agg == 5 ~ 2,
                                                    (cso_agg == 2 & CAT_OCUP >= 3) | cso_agg == 4 | cso_agg == 6 ~ 3,
                                                    cso_agg == 7 ~ 4,
                                                    cso_agg == 8 | cso_agg == 9 ~ 5,
                                                    cso_agg == 10 | cso_agg == 11 ~ 6))

eph_419$clase6_factor <- factor(eph_419$clase6, labels = c("Clase alta", 
                                                           "Clase media - autónoma",
                                                           "Clase media -asalariada",
                                                           "Clase obrera - autónoma",
                                                           "Clase obrera - asalariada",
                                                           "Clase obrera - trabajadores marginales"))

Distribuciones de frecuencias (dplyr)

  • Con la variable ya construida tenemos dos formas (entre muchas) para realizar una distribución de frecuencia con los datos ponderados.

  • En primer lugar mostraremos el ejemplo utilizando funciones del paquete dplyr del tidyverse.


eph_419 %>%
    filter(!is.na(clase6_factor)) %>% #quitamos los casos perdidos del análisis 
    group_by(clase6_factor) %>% #agrupamos los datos por clase
    tally(PONDERA) %>% #hacemos un conteo ponderado
    mutate(porcentaje = round((n/sum(n))*100, digits = 2)) #calculamos el porcentaje
# A tibble: 6 × 3
  clase6_factor                                n porcentaje
  <fct>                                    <int>      <dbl>
1 Clase alta                              134342       1.11
2 Clase media - autónoma                 1908959      15.8 
3 Clase media -asalariada                4497102      37.2 
4 Clase obrera - autónoma                1298505      10.7 
5 Clase obrera - asalariada              3503745      29.0 
6 Clase obrera - trabajadores marginales  760754       6.29

Distribuciones de frecuencias (summarytools)

También podemos utilizar la función freq del paquete summarytools, que debemos instalarlo previamente.

library(summarytools)

freq(eph_419$clase6_factor, weights = eph_419$PONDERA, cumul = FALSE, report.nas = FALSE)
Weighted Frequencies  
eph_419$clase6_factor  
Type: Factor  
Weights: PONDERA  

                                                      Freq        %
-------------------------------------------- ------------- --------
                                  Clase alta     134342.00     1.11
                      Clase media - autónoma    1908959.00    15.77
                     Clase media -asalariada    4497102.00    37.16
                     Clase obrera - autónoma    1298505.00    10.73
                   Clase obrera - asalariada    3503745.00    28.95
      Clase obrera - trabajadores marginales     760754.00     6.29
                                       Total   12103407.00   100.00

6. Explorando resultados. Tablas y gráficos

Clases e ingresos (I)

  • Tomando como variable dependiente los ingresos totales individuales (P47T), calcularemos el promedio por clase social.

  • Para ello utilizaremos algunas funciones del paquete dplyr y de R base como weighted.mean.

eph_419 %>% 
  filter(!is.na(clase6_factor)) %>%  # Quitamos los casos que no tienen clase social
  group_by(clase6_factor) %>% # Agrupamos por clase
  summarise(media = weighted.mean(P47T, w = PONDII)) # Calculamos el promedio ponderado
# A tibble: 6 × 2
  clase6_factor                           media
  <fct>                                   <dbl>
1 Clase alta                             76779.
2 Clase media - autónoma                 33651.
3 Clase media -asalariada                37616.
4 Clase obrera - autónoma                19315.
5 Clase obrera - asalariada              24375.
6 Clase obrera - trabajadores marginales 12578.

Clases e ingresos (II)

  • Otra forma de observar las desigualdades es a través de gráficos

  • En este caso, a través del paquete ggplot2 del tidyverse, construiremos paso a paso un diagrama de cajas y bigotes (boxplot).

eph_419 %>%
  filter(!is.na(clase6_factor), P47T < 150000) %>% 
  ggplot(aes(x=clase6_factor, y=P47T, fill=clase6_factor, weight = PONDII)) +
  geom_boxplot(outlier.alpha = 0.1, show.legend = FALSE) +
  labs(title = "Ingresos totales individuales por clase social. Argentina urbana 2019",
    y = "Ingresos totales individuales",
       caption = "Elaboración propia en base a EPH-INDEC 2019") +
  theme(plot.caption = element_text(size = 10),
        plot.title = element_text(size = 14),
        axis.title.x = element_blank(),
        axis.title.y = element_text(size = 12),
        axis.text.x = element_text(size = 12),
        axis.text.y = element_text(size = 12)) +
  scale_x_discrete(labels = function(x) str_wrap(x, width = 20)) +
  scale_y_continuous(breaks=seq(0, 150000, 10000))

Clases e ingresos (II)

Las clases en el tiempo (I)

  1. Podemos analizar como ha evolucionado la estructura de clases en su composición

  2. Para ello, vamos a descargar las bases de la EPH del tercer trimestre entre 2018 y 2022.

eph_1822 <- get_microdata(year = 2018:2022, trimester = 3, type = "individual") # Descargamos el pool de bases

table(eph_1822$ANO4) # Exploramos los casos por año

 2018  2019  2020  2021  2022 
56879 57229 41685 48668 49232
  1. Luego aplicaremos el script para la creación del sistema de clases sociales a esta nueva base.
  1. A continuación mostraremos los resultados en una tabla cruzada y en un gráfico de barras apiladas.

Las clases en el tiempo (III)

  • Podemos construir la tabla usando las funciones del paquete dplyr.

  • La función spread permite pasar a un formato ancho de tabla.

eph_1822 %>%
  filter(!is.na(clase6_factor)) %>% #Filtramos a los que no tienen clase
  group_by(ANO4, clase6_factor) %>% #Agrupamos por año y clase
  tally(wt=PONDERA) %>% #Calculamos la frecuencias ponderadas
  group_by(ANO4) %>% #Agrupamos por año
  mutate(percent = round((n/sum(n))*100, digits = 2)) %>% #Calculamos el porcentaje de clase por año
  select(clase6_factor, ANO4, percent) %>% #Seleccionamos las columnas con las que nos quedaremos
  spread(ANO4, value = percent) #Cambiamos a formato ancho de tabla
# A tibble: 6 × 6
  clase6_factor                          `2018` `2019` `2020` `2021` `2022`
  <fct>                                   <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
1 Clase alta                               0.87   0.92   1.03   0.99   0.91
2 Clase media - autónoma                  14.8   15.7   14.8   15.8   15.8 
3 Clase media -asalariada                 36.4   36.3   38.8   39     36.2 
4 Clase obrera - autónoma                 10.1   10.8   12.7   10.8   11.0 
5 Clase obrera - asalariada               31.0   30.0   26.9   27.6   30.7 
6 Clase obrera - trabajadores marginales   6.79   6.35   5.78   5.79   5.39

Las clases en el tiempo (IV)

Otra opción de presentación es la elaboración de un gráfico de barras. Para ello recurriremos al paquete ggplot2 y a la función geom_col.

eph_1822 %>%
  filter(!is.na(clase6_factor)) %>% #Aplicamos los mismos pasos que para el cuadro
  group_by(ANO4, clase6_factor) %>% 
  tally(wt=PONDERA) %>% 
  group_by(ANO4) %>% 
  mutate(percent = round((n/sum(n))*100, digits = 2)) %>% 
  ggplot(mapping = aes(x = ANO4, y = percent, fill = clase6_factor)) + #Indicamos qué variables tomará el gráfico
  geom_col() + #Usaremos columnas
  geom_text(aes(label = percent), position = position_stack(.5), size = 3) + #Agregamos los porcentajes en las columnas
  scale_fill_discrete(labels = function(x) str_wrap(x, width = 25)) +
  labs(title = "Evolución de la estructura de clases sociales",
       subtitle = "Población ocupada. Argentina urbana 2018-2022.",
       caption = "Fuente: Elaboración propia en base a EPH-INDEC 2018-2022.",
       fill = "Clase social") +
  theme(legend.title = element_text(size = 10, face = "bold"),
        legend.text = element_text(size = 11),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        axis.text.y = element_text(size = 10),
        axis.text.x = element_text(size = 10),
        plot.title = element_text(size = 14, face = "bold"),
        plot.subtitle = element_text(size = 12),
        plot.caption = element_text(size = 10, hjust = 1)) +
  scale_x_continuous(breaks = c(2018:2022)) +
  scale_y_continuous(breaks=seq(0, 100, 10))

Las clases en el tiempo (IV)

Otros ejemplos de gráficos (I)

Evolución de la pobreza por clase social. Argentina Urbana 2016-2021

Otros ejemplos de gráficos (II)

Percepción de clase social en Argentina. 1995-2017

Otros ejemplos de gráficos (III)

Porcentaje de hogares propietarios de la vivienda según clase social. CABA 2015.

Otros ejemplos de gráficos (IV)

Transiciones de clase. Argentina urbana, 1er y 2do trimestre 2020 - 2021. Población mayor de 18 años.

7. Dudas y consultas